Semilogarithmic graph paper consists of grids in which the horizontal lines are spaced linearly and the vertical lines are spaced logarithmically. (Of course, if you wish to reverse the axes you may simply rotate the graph by 90 degrees.) Many natural phenomena involve relationships that are best described by exponential functions of the form
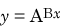. Such relationships are particularly easy to handle by taking logarithms of both sides to obtain a linear relationship between
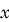and
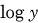; semilogarithmic graph paper is designed to allow you to plot such relationships without needing to compute logarithms of the
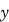values. Plotting the
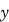values in accordance with the gradations on the logarithmic axis yields the same graph that you would obtain by calculating the logarithm of
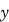and plotting this against
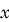on ordinary (linear) graph paper.
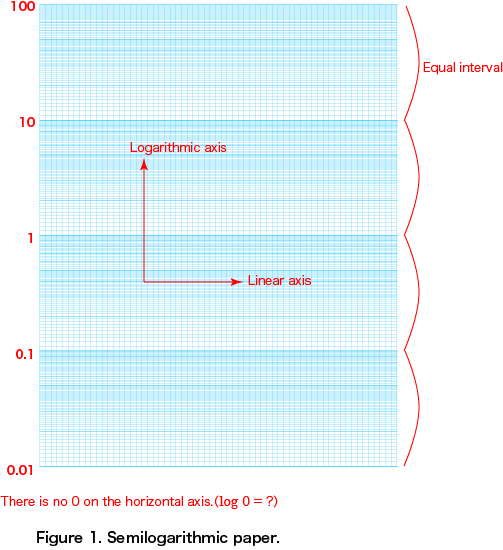
Careful inspection of the vertical axis (logarithmic axis) of semilogarithmic graph paper reveals four equally-spaced intervals, as shown in the figure. The fact that these intervals are evenly spaced logarithmically means that the gaps between each interval correspond to one digit (
,
,
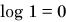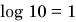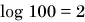, etc.).see Note In the example of Figure 1 to the left, we have labeled the gradations as running from 0.01 (10
-2) to 100 (10
2); however, you could equally as well start the labeling at 1 or 100 or any other power of 10. By thinking about the value of
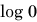, you can quickly understand why there is no point on the vertical axis corresponding to the value 0.
To understand what is going on with the non-evenly-spaced gradation lines on the semilogarithmic graph paper, consider Figure 2. As you can see immediately from this figure, the lines are nothing but logarithmically-spaced gradations.
However, note that actual graph paper also contains secondary gradations distributed finely between 1 and 2.
Note: Perhaps you are thinking
Wait! Doesn’t
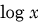denote the natural (base-e) logarithm, while for base-10 logarithms one needs to write
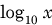? If so, please see the section titled
Notation for logarithms.