When you studied logarithms in mathematics classes, you were probably taught that the notation “
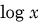” denoted the natural (base-e) logarithm, and that for base-10 logarithms one must write
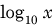. This is absolutely correct, and in the world of mathematics or theoretical physics, the notation “
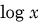” does indeed denote the natural logarithm.
However, in many fields of applied science—including experimental science and engineering—it is conventional to use the notation “
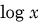” to denote the base-10 logarithm (known as the
common logarithm), while the natural (base-
e) logarithm is denoted “
”.
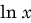How did this confusing situation come to pass? Probably the easiest answer is that natural logarithms are convenient for analytical derivations, while common logarithms are much more intuitive for actually evaluating (or estimating) values of logarithms. Whichever of these two options is more commonly used in any given field is the one to which the standard notation is assigned.